~~ 速報!!あぜりあGenius算数が変わる!! ~~
Genius算数+プログラミング的思考教育クラス

数学IQを養う
保護者の皆様こんな経験ないですか・・・①中学・高校の数学の図形問題。解説を見ても、一向にわからない
②計算はできるんだけど、文章問題になると…できなくなる。
③ひらめきがないと解けない問題を目の当たりにし、算数・数学に挫折した
 生徒にそんな思いさせません!
生徒にそんな思いさせません!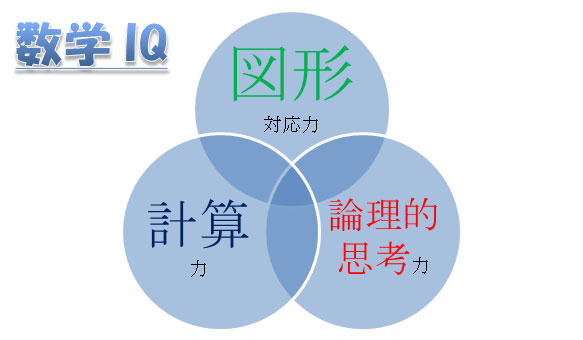
Geniusは、数学IQを上記の三つと定義し、それらを伸ばすことを最優先で行います。
クラス
Genius 1…小学校1・2年生の学習範囲
Genius 2…数学IQ(初級) + 小学校3年生の学習範囲
Genius 3…数学IQ(中級) 図形・論理的思考能力を中心に伸ばします。
Genius 4…数学IQ(中級) + プログラミング的思考基礎
Genius 5…数学IQ(上級) + プログラミング的思考
Genius 6…数学IQ(上級) + プログラミング的思考
Genius算数 1・2・3
| あぜりあ きっての ネイティブ講師が |
| Genius1・2・3は担当します! |
| ・英語のシャワーを浴びながら |
| ・英語で書いてある問題を解く! |
| そして、数学IQを上げる! |
| あぜりあ School だからできること!! |
| それが…Genius算数クラス |
Genius算数 4・5・6
文部科学省: プログラミング教育を必修化決定(2020年度から)
必修化するねらい

「プログラミング的思考とは?」
…
コンピュータに命令を出すときのように
=> ゴールを設定し、
=> 順序立てて物事を考え、
=> 実行に移す力
のことです。
=> ゴールを設定し、
=> 順序立てて物事を考え、
=> 実行に移す力
のことです。
あぜりあ 
プログラミング的思考を取り込んだ算数・数学的思考の育成を目指します!!
【数学IQ + プログラミング的思考教育】は2020年4月より導入します。
| Genius Vision | |
| 例1 | 中学入試に対応できる! 図形・文章題。気づく!ひらめく!理解できる! |
| 例2 | 高校入試のアドバンテージができる! 中学生になった時、定期テストが簡単に思える。高校入試の難問が難なく解ける! |
| Genius 効果例 | |
| ① 昨年度入試では、4月時の偏差値40前後の小学6年生が、(たった1年足らずで) 千葉大附属【偏差値69程度】に合格した! | |
| ② 論理的思考能力の改善により、文章問題が得意になった! | |
| ③ 高校受験時に、ある程度の図形の問題なら、一瞬で答えがわかるようになった! | |
| などなど。 | |
ご興味があれば、直接ご相談ください。(内容が特殊なため、適正人数がございます。ご了承ください。)
開催校:京成津田沼本校・西船橋校・本八幡校
下記のものは、実際にGenius2の問題です。保護者の皆様、是非挑戦してみて下さい。
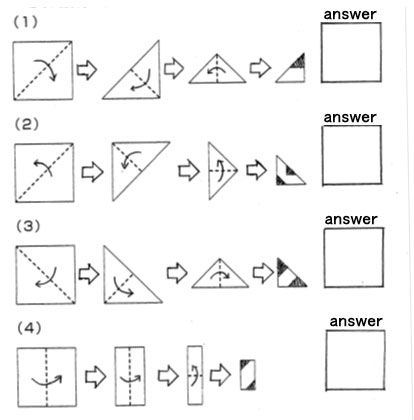
算数脳の内、図形を見る力の基礎的な問題です。
| Seeing patterns |
| A square piece of paper is folded as shown along the dotted lines. If the dark sections are then cut away and the paper unfolded, what will be the result? Please show your answer by outlining and shading in the cut away portions in the space provided. |
 |
お次は、論理的思考能力の問題。ヒントは、全体です!☆頑張ってください☆
| Q.Follow the rules below and fill in the empty squares. |
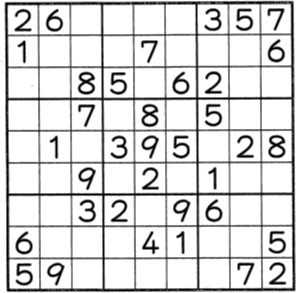 |
| Rules 1) Each small individual square can contain a single digit from 1 to 9. 2) Each of the nine rows and nine columns contains all the digits from 1 to 9. 3) Each 3*3 block of small squares outlined by the thicker lines contains all the digits from 1 to 9. |
Geniusで力をつけると、こんな問題に対応できます!
| 県立千葉中 H22年度 の問題 |
| (2)とも子さんが、月曜日、火曜日、木曜日、土曜日に活動したと考えられる内容を、下の〔表し方の例〕にならって、(月曜日の内容、火曜日の内容、木曜日の内容、土曜日の内容)の順に、すべて書きなさい。 〔表し方の例〕 (歩道と花だん、公園、公園と花だん、リサイクル) 切り紙もよう |
| とも子さんは、もらった地域元気券を箱に入れようと考えました。そして、その箱をかざるために、次のように切り紙もようを作りました。 とも子:図1のように、9×9の正方形のマス目の紙を用紙したよ。 まず、1回目に、アの点線で内側に折り(①)、2回目に、イの点線で内がわに折り重ねるよ(②)。 |
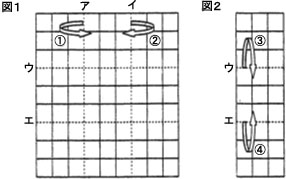 |
| お母さん:図2のようになったんだね。 とも子:うん、そして、3回目にウの点線で内がわへ折り(③)、4回目に、エの点線で 内がわに折り重ねるよ(④)。
お父さん:図3のようになったんだね。 |
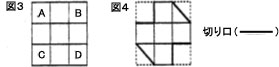 |
| とも子:そこで、まず図3のAのマスとDのマスで重なっている部分をすべて切り落とし、 次にBのマスとCのマスで重なっている部分をななめに、すべて切り落として、図4のようにしたわ。
お母さん:紙をもとのように開いたら、どのような切り紙が出来たのかな。 |
| (3)図3において、Aのマスで重なっている部分は、もとの紙ではどのマスにあたるのか、そのマスすべてを下の図アに、Aと書き入れなさい。 *問題用紙や解答用紙などを、実際に折って考えてはいけません。 |
| 開成中 某年度 の問題 |
| AB=6cm、BC=7cmの三角形ABCの辺BC上に点Dをとり、三角形ABCを2点AとDを通る 直線で折り返すと、点Bは右上のような点Bに重なります。AEとBCの交わる点をFとすると、 CF=3cmになり、三角形ABCの面積が三角形DEFの面積の7倍になります。 |
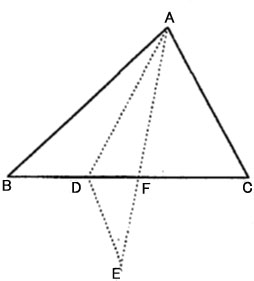 |
| (1)AF、BDの長さをそれぞれ求めなさい。 |
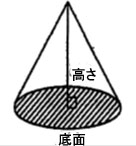
| (2)三角形ACDを2点AとDを通る直線を軸として回転してできる立体の体積は、三角形 ABDを2点AとDを通る直線を軸として回転してできる立体の体積の何倍ですか。ただし、 下の図のような立体を「円すい」といい、その体積は (底面の円の面積)×(高さ)÷3
で求めることができます。 |
 |






